Eight queens puzzle

	a	b	c	d	e	f	g	h
8	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$		${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	8
7	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$		${{{square}}} __$	7
6	${{{square}}} __$	${{{square}}} __$		${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	6
5	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$		5
4	${{{square}}} __$		${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	4
3	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$		${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	3
2		${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	2
1	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$	${{{square}}} __$		${{{square}}} __$	${{{square}}} __$	1
	a	b	c	d	e	f	g	h

One solution.

The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard such that none of them are able to capture any other using the standard chess queen's moves. The queens must be placed in such a way that no two queens attack each other. Thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general n-queens problem of placing n queens on an n×n chessboard, where solutions exist only for n = 1 or n ≥ 4.

1 History
2 Constructing a solution
3 Solutions to the eight queens puzzle
4 Counting solutions
5 Related problems
6 The eight queens puzzle as an exercise in algorithm design
7 An animated version of the recursive solution
8 See also
9 References
10 External links
- 10.1 Links to solutions

History

The puzzle was originally proposed in 1848 by the chess player Max Bezzel, and over the years, many mathematicians, including Gauss, have worked on this puzzle and its generalized n-queens problem. The first solutions were provided by Franz Nauck in 1850. Nauck also extended the puzzle to n-queens problem (on an n×n board—a chessboard of arbitrary size). In 1874, S. Günther proposed a method of finding solutions by using determinants, and J.W.L. Glaisher refined this approach.

Edsger Dijkstra used this problem in 1972 to illustrate the power of what he called structured programming. He published a highly detailed description of the development of a depth-first backtracking algorithm.²

Constructing a solution

The problem can be quite computationally expensive as there are 4,426,165,368 (i.e., 64 choose 8) possible arrangements of eight queens on a 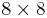$8\times8$ board, but only 92 solutions. It is possible to use shortcuts that reduce computational requirements or rules of thumb that avoids brute force computational techniques. For example, just by applying a simple rule that constrains each queen to a single column (or row), though still considered brute force, it is possible to reduce the number of possibilities to just 16,777,216 (that is, 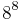$8^8$ ) possible combinations. Generating the permutations that are solutions of the eight rooks puzzle^[1] and then checking for diagonal attacks further reduces the possibilities to just 40,320 (that is, 8!). These are computationally manageable for n = 8, but would be intractable for problems of n ≥ 20, as 20! = 2.433 * 10¹⁸. Extremely interesting advancements for this and other toy problems is the development and application of heuristics (rules of thumb) that yield solutions to the n queens puzzle at an astounding fraction of the computational requirements. This heuristic solves n queens for any n n ≥ 4 or n = 1:

Divide n by 12. Remember the remainder (n is 8 for the eight queens puzzle).
Write a list of the even numbers from 2 to n in order.
If the remainder is 3 or 9, move 2 to the end of the list.
Append the odd numbers from 1 to n in order, but, if the remainder is 8, switch pairs (i.e. 3, 1, 7, 5, 11, 9, …).
If the remainder is 2, switch the places of 1 and 3, then move 5 to the end of the list.
If the remainder is 3 or 9, move 1 and 3 to the end of the list.
Place the first-column queen in the row with the first number in the list, place the second-column queen in the row with the second number in the list, etc.

For n = 8 this results in the solution shown above. A few more examples follow.

14 queens (remainder 2): 2, 4, 6, 8, 10, 12, 14, 3, 1, 7, 9, 11, 13, 5.
15 queens (remainder 3): 4, 6, 8, 10, 12, 14, 2, 5, 7, 9, 11, 13, 15, 1, 3.
20 queens (remainder 8): 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 3, 1, 7, 5, 11, 9, 15, 13, 19, 17.

Solutions to the eight queens puzzle

The eight queens puzzle has 92 distinct solutions. If solutions that differ only by symmetry operations (rotations and reflections) of the board are counted as one, the puzzle has 12 unique (or fundamental) solutions, which are presented below:

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 1

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 2

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 3

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 4

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 5

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 6

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 7

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 8

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 9

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 10

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 11

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Unique solution 12

Counting solutions

The following table gives the number of solutions for placing n queens on an n × n board, both unique (sequence A002562 in OEIS) and distinct (sequence A000170 in OEIS), for n=1–14, 24–26.

n:	1	2	3	4	5	6	7	8	9	10	11	12	13	14	..	24	25	26
unique:	1	0	0	1	2	1	6	12	46	92	341	1,787	9,233	45,752	..	28,439,272,956,934	275,986,683,743,434	2,789,712,466,510,289
distinct:	1	0	0	2	10	4	40	92	352	724	2,680	14,200	73,712	365,596	..	227,514,171,973,736	2,207,893,435,808,352	22,317,699,616,364,044

Note that the six queens puzzle has fewer solutions than the five queens puzzle.

There is currently no known formula for the exact number of solutions.

The eight queens puzzle as an exercise in algorithm design

Finding all solutions to the eight queens puzzle is a good example of a simple but nontrivial problem. For this reason, it is often used as an example problem for various programming techniques, including nontraditional approaches such as constraint programming, logic programming or genetic algorithms. Most often, it is used as an example of a problem which can be solved with a recursive algorithm, by phrasing the n queens problem inductively in terms of adding a single queen to any solution to the problem of placing n−1 queens on an n-by-n chessboard. The induction bottoms out with the solution to the 'problem' of placing 0 queens on an n-by-n chessboard, which is the empty chessboard.

This technique is much more efficient than the naïve brute-force search algorithm, which considers all 64⁸ = 2⁴⁸ = 281,474,976,710,656 possible blind placements of eight queens, and then filters these to remove all placements that place two queens either on the same square (leaving only 64!/56! = 178,462,987,637,760 possible placements) or in mutually attacking positions. This very poor algorithm will, among other things, produce the same results over and over again in all the different permutations of the assignments of the eight queens, as well as repeating the same computations over and over again for the different sub-sets of each solution. A better brute-force algorithm places a single queen on each row, leading to only 8⁸ = 2²⁴ = 16,777,216 blind placements.

It is possible to do much better than this. One algorithm solves the eight rooks puzzle by generating the permutations of the numbers 1 through 8 (of which there are 8! = 40,320), and uses the elements of each permutation as indices to place a queen on each row. Then it rejects those boards with diagonal attacking positions. The backtracking depth-first search program, a slight improvement on the permutation method, constructs the search tree by considering one row of the board at a time, eliminating most nonsolution board positions at a very early stage in their construction. Because it rejects rook and diagonal attacks even on incomplete boards, it examines only 15,720 possible queen placements. A further improvement which examines only 5,508 possible queen placements is to combine the permutation based method with the early pruning method: the permutations are generated depth-first, and the search space is pruned if the partial permutation produces a diagonal attack. Constraint programming can also be very effective on this problem.

An alternative to exhaustive search is an 'iterative repair' algorithm, which typically starts with all queens on the board, for example with one queen per column. It then counts the number of conflicts (attacks), and uses a heuristic to determine how to improve the placement of the queens. The 'minimum-conflicts' heuristic — moving the piece with the largest number of conflicts to the square in the same column where the number of conflicts is smallest — is particularly effective: it solves the 1,000,000 queen problem in less than 50 steps on average. This assumes that the initial configuration is 'reasonably good' — if a million queens all start in the same row, it will obviously take at least 999,999 steps to fix it. A 'reasonably good' starting point can for instance be found by putting each queen in its own row and column such that it conflicts with the smallest number of queens already on the board.

Note that 'iterative repair', unlike the 'backtracking' search outlined above, does not guarantee a solution: like all hillclimbing (i.e., greedy) procedures, it may get stuck on a local optimum (in which case the algorithm may be restarted with a different initial configuration). On the other hand, it can solve problem sizes that are several orders of magnitude beyond the scope of a depth-first search.

An animated version of the recursive solution

This animation uses backtracking to solve the problem. A queen is placed in a column that is known not to cause conflict. If a column is not found the program returns to the last good state and then tries a different column.

Algorithms that solve the eight queens puzzle implemented in different programming languages are found in the eight queens puzzle solutions article.

References

↑ Rooks Problem from Wolfram MathWorld
↑ G. Polya, Uber die “doppelt-periodischen” Losungen des n-Damen-Problems, George Polya: Collected papers Vol. IV, G-C. Rota, ed., MIT Press, Cambridge, London, 1984, pp. 237–247

Bell, Jordan and Stevens, Brett, A survey of known results and research areas for n-queens, Discrete Mathematics, Vol. 309, Issue 1, 6 January 2009, 1-31.
Watkins, John J. (2004). Across the Board: The Mathematics of Chess Problems. Princeton: Princeton University Press. ISBN 0-691-11503-6.
O.-J. Dahl, E. W. Dijkstra, C. A. R. Hoare Structured Programming, Academic Press, London, 1972 ISBN 0-12-200550-3 see pp 72–82 for Dijkstra's solution of the 8 Queens problem.
Three Dimensional NxN-Queens Problems, L.Allison, C.N.Yee, & M.McGaughey (1988), Department of Computer Science, Monash University, Australia.
S. Nudelman, The Modular N-Queens Problem in Higher Dimensions, Discrete Mathematics, vol 146, iss. 1-3, 15 November 1995, pp. 159–167.
On The Modular N-Queen Problem in Higher Dimensions, Ricardo Gomez, Juan Jose Montellano and Ricardo Strausz (2004), Instituto de Matematicas, Area de la Investigacion Cientifica, Circuito Exterior, Ciudad Universitaria, Mexico.
J. Barr and S. Rao, The n-Queens Problem in Higher Dimensions, Elemente der Mathematik, vol 61 (2006), pp. 133–137.

Eight queens puzzle

Contents

History

Constructing a solution

Solutions to the eight queens puzzle

Counting solutions

Related problems

The eight queens puzzle as an exercise in algorithm design

An animated version of the recursive solution

See also

References

External links

Links to solutions